Cognitive dysfunction
Cognitive dysfunction or cognitive impairment is a symptom in most diagnostic criteria for ME/CFS; some patients call it "brain fog".[1][2] It is also a common symptom of fibromyalgia which many patients call "fibro fog."[3]
Forms of cognitive dysfunction commonly found in ME/CFS include reduced attention span,[4][5] brain fog/cognitive fog,[1][6] cognitive overload,[6] concentration problems,[7] confusion,[7] difficulties with calculations,[6][5] dyslexia (or linguistic reversals) when fatigued,[7][6] difficulty absorbing information,[7] difficulty sequencing words and numbers,[7] multi-tasking problems,[8][7] planning problems, poor working memory,[6][7] reading or speaking difficulties,[6] short-term memory problems,[7][6] slowed thought,[7][6] spatial disorientation,[5] slow processing of information[7] and word-finding problems.[7] A 2016 study found that IQ scores of adolescents with CFS tested lower than the IQ scores of healthy peers with an equivalent school level. Currently it is not known whether lower IQ outcomes are due to concentration problems, a lowered processing speed or the illness itself.[9]
Prevalence[edit | edit source]
Cognitive dysfunction is extremely common in ME/CFS, and is a symptom used for diagnosis in most case definitions including the current CDC diagnostic criteria for ME/CFS.
Cognitive dysfunction is also a symptom that commonly occurs during post-exertional malaise, which is the hallmark symptom of ME/CFS, and can result from orthostatic intolerance, which is another very common ME/CFS symptom.[6][10]
Symptom recognition[edit | edit source]
Cognitive dysfunction is a particularly common symptom of ME/CFS, but is also a symptom of many other illnesses.
Mandatory ME/CFS symptom[edit | edit source]
Cognitive dysfunction is a mandatory diagnostic symptom for ME/CFS with the Canadian Consensus Criteria (CCC).[6]
Optional ME/CFS symptom[edit | edit source]
Impaired memory or ability to concentrate is a core symptom in the current CDC ME/CFS diagnostic criteria diagnostic criteria, and is required when orthostatic intolerance is not present.[11] Cognitive dysfunction is part of the possible diagnostic symptoms in the International Consensus Criteria (ICC) for myalgic encephalomyelitis (ME).[12]
Other causes[edit | edit source]
Diagnosis[edit | edit source]
Possible causes[edit | edit source]
Neurological changes in ME/CFS[edit | edit source]
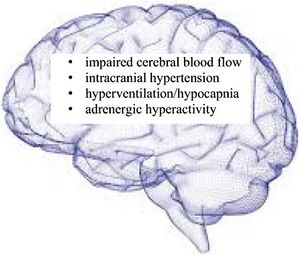
Source: Wirth, K.J., Scheibenbogen, C. & Paul, F. An attempt to explain the neurological symptoms of Myalgic Encephalomyelitis/Chronic Fatigue Syndrome. J Transl Med 19, 471 (2021). https://doi.org/10.1186/s12967-021-03143-3
Causes of neurological symptoms in ME/CFS include:
- hyperventilation/hypnocapnia (reduced carbon dioxide levels in the blood)
- intracranial hypertension (increased pressure within the skull and around brain)
- reduced blood flow to the brain
- brain inflammation may also be a factor[13]
Wirth, Scheibenbogen and Paul (2021) state these "can explain cognitive impairment, brain fog, headache, psychomotor slowing, ataxia and loss of coordination of movements, hypersensitivity, sleep disturbances and dysautonomia."[13]
Cerebrospinal fluid changes[edit | edit source]
Mady Hornig and colleagues have found evidence in the cerebrospinal fluid (CSF) of ME/CFS patients that may explain their cognitive dysfunction.[14]
Brain changes[edit | edit source]
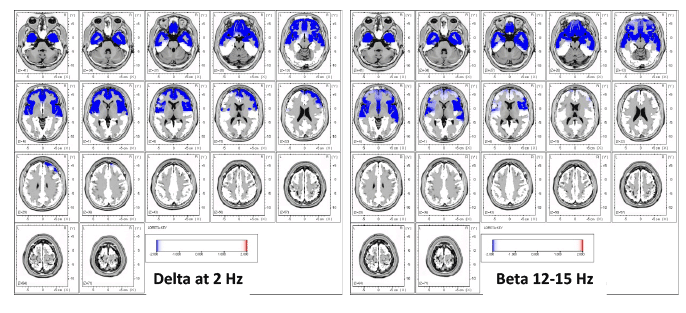
Zinn et al. (2016) studied brain functioning in chronic fatigue syndrome and concluded:
Our case study confirmed the pattern of dysregulation in the cortex reviewed in the introduction. Furthermore, since both periods of phase shift/lock durations were found to be significantly shorter, that might contribute to an increased rate of phase reset, also seen in our data. Phase reset deregulation--phase locking periods being too brief and phase reset happening too often—appear to be consistent with the associated lower rate of information processing and reaction times found in the ME and CFS literature. These deregulated states represent the brain during nonoptimal functioning, rendering it inefficient for most types of information processing functioning, whether it is executive functioning, memory, perceptual reasoning or information processing speed. When phase lock is significantly less than normal, as in this data set, the ability of the brain to sustain commitment of resources to mediate different functions is severely compromised. Phase shift duration in this data is also hypoactive, meaning that significantly less neurons are being recruited to perform a function than normal. The results here indicate slowed verbal comprehension, executive functions, perceptual reasoning, processing speed and memory, the sum total of which is known as cognitive impairment.[15]
Drug and supplements[edit | edit source]
Drugs, supplements or treatment interventions that may cause cognitive problems in some ME/CFS patients:
- Diphenhydramine (Benadryl) an antihistamine also used to aid sleep
- Certain pain killers, particularly opioids, gabapentin (Neurontin), tricyclic antidepressants including amitriptyline (Elavil, Endep) and nortriptyline (Aventyl, Pamelor)[16]
- sleep medications[16]
Exercise and graded exercise therapy[edit | edit source]
A healthy person becomes more alert after exercise, but people with ME/CFS find their cognitive difficulties increase, they become much slower at mental activities, and cognitive tasks seem to take extra effort.[7][6][17] Graded exercise therapy (GET) / Graded Activity Therapy also has this effect in ME/CFS patients.[7][6][17]
Other illnesses or health conditions[edit | edit source]
Cognitive dysfunction can be caused or made worse by other health conditions, most of which should be ruled out or identified during diagnostic process for ME/CFS:
- Cancer or cancer treatment ("chemo brain")
- Depression
- Fibromyalgia
- Long COVID symptoms[18]
- Lupus
- Menopause
- Multiple sclerosis
- Pregnancy
- Sleep dysfunction or sleep disorders[19]
Potential treatments[edit | edit source]
Drugs, supplements and other treatments that have been suggested for reducing cognitive impairment and/or improving brain fog include:
- Acetyl-L-carnitine[17]
- Arabinoxylan (ineffective)[17]
- B vitamin complex
- B vitamin
- Clonidine hydrochloride (ineffective)[17]
- Dexamphetamine (weak evidence)[6]
- Dynamic Neural Retraining System
- Fludrocortisone (ineffective)[17]
- Histamine
- Hydrocortisone (most trials show some positive effective)[17]
- Lying down or moving to a semi-reclined position for cognitive tasks[6]
- Methylene blue
- Methylphenidate (weak evidence)[6] and the experimental treatment KPAX002[20]
- Modafinil for alertness[6] but Collatz et al. (2014) found it ineffective[17]
- Moclobemide[17]
- Neurolinguistic programming
- Nimodipine for mental clarity, starting at 30mg, increase up to 60mg if tolerated (weak evidence)[6]
- Phenelzine (ineffective in ME/CFS)[17]
- Rintatolimod (Ampligen)
- Stellate ganglion block in dysautonomia in some long COVID patients
- Valganciclovir (ineffective)[17]
- Yoga
Notable studies[edit | edit source]
- 2022, Systematic review and meta‐analysis of cognitive impairment in myalgic encephalomyelitis/chronic fatigue syndrome (ME/CFS)[21] - (Full text)
- 2016, Cognitive Dysfunction in Chronic Fatigue Syndrome: a Review of Recent Evidence[22] - (Abstract)
- 2016, The impact of chronic fatigue syndrome on cognitive functioning in adolescents[9] - (Full text)
- 2016, qEEG / LORETA in Assessment of Neurocognitive Impairment in a Patient with Chronic Fatigue Syndrome: A Case Report[15] - (Full text)
- 2011, Cognitive deficits in patients with chronic fatigue syndrome compared to those with major depressive disorder and healthy controls[4] - (Full text)
- 2006, Cognitive dysfunction relates to subjective report of mental fatigue in patients with chronic fatigue syndrome[23] - (Full text)
- 2015, Less efficient and costly processes of frontal cortex in childhood chronic fatigue syndrome[8] - (Full Text)
- 2001, Neuropsychological functioning in chronic fatigue syndrome: a review - (Abstract)[24]
Disability[edit | edit source]
In 2018 Brian Vastag was able to prove the severity of his chronic fatigue syndrome cognitive dysfunction with qEEG and cognitive tests, which proved he had "significant problems with visual perception and analysis, scanning speed, attention, visual motor coordination, motor and mental speed, memory, and verbal fluency" winning his long term disability (LTD) claim in the United States.[25]
See also[edit | edit source]
- Fibromyalgia
- Long COVID
- Aphasia
- Dyscalculia
- Dysphasia
- Memory problems
- Word-finding problems
- Myalgic encephalomyelitis (M.E.)
- Long COVID
Learn more[edit | edit source]
- 2015, Dr. Gudrun Lange Reviews Neuropsychological Testing for CFS and FM
- 2016, Case Study: "Brain Fog" in CFS can be seen in qEEG/Loreta
- 2018, Study Identifies the Types of Cognitive Dysfunction That Are Most Prevalent in Fibromyalgia
- Jun 4, 2018, Victory For ME Disability Claim – U.S. Court Upholds Plaintiff's Lawsuit After Being Denied Disability
References[edit | edit source]
- ↑ 1.0 1.1 Jason, Leonard A.; Sunnquist, Madison; Brown, Abigail; Evans, Meredyth; Vernon, Suzanne D.; Furst, Jacob D.; Simonis, Valerie (2014), "Examining case definition criteria for chronic fatigue syndrome and myalgic encephalomyelitis", Fatigue: Biomedicine, Health & Behavior, 2 (1): 40-56, doi:10.1080/21641846.2013.862993
- ↑ Kingdon, Caroline; Giotas, Dionysius; Nacul, Luis; Lacerda, Eliana (September 2020). "Health Care Responsibility and Compassion-Visiting the Housebound Patient Severely Affected by ME/CFS". Healthcare. 8 (3): 197. doi:10.3390/healthcare8030197. PMC 7551603. PMID 32635535.
- ↑ Kravitz, Howard M.; Katz, Robert S. (July 1, 2015). "Fibrofog and fibromyalgia: a narrative review and implications for clinical practice". Rheumatology International. 35 (7): 1115–1125. doi:10.1007/s00296-014-3208-7. ISSN 1437-160X.
- ↑ 4.0 4.1 Constant, E.L.; Adam, S.; Gillain, B.; Lambert, M.; Masquelier, E.; Seron, X. (May 1, 2011). "Cognitive deficits in patients with chronic fatigue syndrome compared to those with major depressive disorder and healthy controls". Clinical Neurology and Neurosurgery. 113 (4): 295–302. doi:10.1016/j.clineuro.2010.12.002. ISSN 0303-8467.
- ↑ 5.0 5.1 5.2 De Becker, Pascale; McGregor, Neil; De Meirleir, Kenny (December 2001). "A definition‐based analysis of symptoms in a large cohort of patients with chronic fatigue syndrome". Journal of Internal Medicine. 250 (3): 234–240. doi:10.1046/j.1365-2796.2001.00890.x.
- ↑ 6.00 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.10 6.11 6.12 6.13 6.14 6.15 6.16 Carruthers, Bruce M.; Jain, Anil Kumar; De Meirleir, Kenny L.; Peterson, Daniel L.; Klimas, Nancy G.; Lerner, A. Martin; Bested, Alison C.; Flor-Henry, Pierre; Joshi, Pradip; Powles, AC Peter; Sherkey, Jeffrey A.; van de Sande, Marjorie I. (2003). "Myalgic Encephalomyelitis/Chronic Fatigue Syndrome: Clinical Working Case Definition, Diagnostic and Treatment Protocols" (PDF). Journal of Chronic Fatigue Syndrome. 11 (2): 7–115. doi:10.1300/J092v11n01_02.
- ↑ 7.00 7.01 7.02 7.03 7.04 7.05 7.06 7.07 7.08 7.09 7.10 7.11 7.12 Carruthers, BM; van de Sande, MI; De Meirleir, KL; Klimas, NG; Broderick, G; Mitchell, T; Staines, D; Powles, ACP; Speight, N; Vallings, R; Bateman, L; Bell, DS; Carlo-Stella, N; Chia, J; Darragh, A; Gerken, A; Jo, D; Lewis, DP; Light, AR; Light, KC; Marshall-Gradisnik, S; McLaren-Howard, J; Mena, I; Miwa, K; Murovska, M; Stevens, SR (2012), Myalgic encephalomyelitis: Adult & Paediatric: International Consensus Primer for Medical Practitioners (PDF), ISBN 978-0-9739335-3-6
- ↑ 8.0 8.1 Mizuno, Kei; Tanaka, Masaaki; Tanabe, Hiroki C.; Joudoi, Takako; Kawatani, Junko; Shigihara, Yoshihito; Tomoda, Akemi; Miike, Teruhisa; Imai-Matsumura, Kyoko (September 10, 2015). "Less efficient and costly processes of frontal cortex in childhood chronic fatigue syndrome". NeuroImage : Clinical. 9: 355–368. doi:10.1016/j.nicl.2015.09.001. ISSN 2213-1582. PMID 26594619.
- ↑ 9.0 9.1 Nijhof, Linde N.; Nijhof, Sanne L.; Bleijenberg, Gijs; Stellato, Rebecca K.; Kimpen, Jan L.L.; Pol, Hilleke E. Hulshoff; van de Putte, Elise M.; E (February 2016). "The impact of chronic fatigue syndrome on cognitive functioning in adolescents". European Journal of Pediatrics. 175 (2): 245–252. doi:10.1007/s00431-015-2626-1. ISSN 0340-6199. PMC 4724362. PMID 26334394.
- ↑ 10.0 10.1 Arnold, Amy (February 3, 2016). "Cognitive Dysfunction and "Brain Fog" in POTS | The Dysautonomia Dispatch". Dysautonomia International. Retrieved August 28, 2018.
- ↑ "IOM 2015 Diagnostic Criteria | Myalgic Encephalomyelitis/Chronic Fatigue Syndrome". Centers for Disease Control and Prevention. January 27, 2021. Retrieved February 25, 2021.
- ↑ Carruthers, BM; van de Sande, MI; De Meirleir, KL; Klimas, NG; Broderick, G; Mitchell, T; Staines, D; Powles, ACP; Speight, N; Vallings, R; Bateman, L; Bell, DS; Carlo-Stella, N; Chia, J; Darragh, A; Gerken, A; Jo, D; Lewis, DP; Light, AR; Light, KC; Marshall-Gradisnik, S; McLaren-Howard, J; Mena, I; Miwa, K; Murovska, M; Stevens, SR (2012), Myalgic encephalomyelitis: Adult & Paediatric: International Consensus Primer for Medical Practitioners (PDF), ISBN 978-0-9739335-3-6
- ↑ 13.0 13.1 Cite error: Invalid
<ref>tag; no text was provided for refs namedWirth2021b - ↑ Hornig, M; Gottschalk, G; Peterson, D; Knox, KK; Schultz, AF; Eddy, ML; Che, X; Lipkin, WI (2016). "Cytokine network analysis of cerebrospinal fluid in myalgic encephalomyelitis/chronic fatigue syndrome". Molecular Psychiatry. 21 (2): 261-9. doi:10.1038/mp.2015.29.
- ↑ 15.0 15.1 15.2 Zinn, ML; Zinn, Mark A.; Jason, Leonard (2016). "qEEG / LORETA in Assessment of Neurocognitive Impairment in a Patient with Chronic Fatigue Syndrome: A Case Report". sciforschenonline.org. SciForschen. doi:10.16966/2469-6714.110. ISSN 2469-6714. Retrieved August 28, 2018.
- ↑ 16.0 16.1 https://www.health.harvard.edu/mind-and-mood/stuck-in-a-brain-fog-look-in-your-medicine-cabinet
- ↑ 17.00 17.01 17.02 17.03 17.04 17.05 17.06 17.07 17.08 17.09 17.10 Collatz, Ansel; Johnston, Samantha C.; Staines, Donald R.; Marshall-Gradisnik, Sonya M. (June 2016). "A Systematic Review of Drug Therapies for Chronic Fatigue Syndrome/Myalgic Encephalomyelitis". Clinical Therapeutics. 38 (6): 1263–1271.e9. doi:10.1016/j.clinthera.2016.04.038. ISSN 1879-114X. PMID 27229907.
- ↑ Soriano, Joan B.; Allan, Maya; Alsokhn, Carine; Alwan, Nisreen A.; Askie, Lisa; Davis, Hannah E.; Diaz, Janet V.; Dua, Tarun; de Groote, Wouter; Jakob, Robert; Lado, Marta; Marshall, John; Murthy, Srin; Preller, Jacobus; Relan, Pryanka; Schiess, Nicoline; Seahwag, Archana (October 6, 2021), A clinical case definition of post COVID-19 condition by a Delphi consensus, World Health Organization (WHO) clinical case definition working group on post COVID-19 condition, World Health Organization
- ↑ "Reasons You May Have Brain Fog". WebMD. Retrieved January 22, 2022.
- ↑ Valdizán Usón, José Ramón; Idiazábal Alecha, María Ángeles (June 1, 2008). "Diagnostic and treatment challenges of chronic fatigue syndrome: role of immediate-release methylphenidate". Expert Review of Neurotherapeutics. 8 (6): 917–927. doi:10.1586/14737175.8.6.917. ISSN 1473-7175.
- ↑ Aoun Sebaiti, Mehdi; Hainselin, Mathieu; Gounden, Yannick; Sirbu, Carmen Adella; Sekulic, Slobodan; Lorusso, Lorenzo; Nacul, Luis; Authier, François Jérôme (February 9, 2022). "Systematic review and meta-analysis of cognitive impairment in myalgic encephalomyelitis/chronic fatigue syndrome (ME/CFS)". Scientific Reports. 12 (1): 2157. doi:10.1038/s41598-021-04764-w. ISSN 2045-2322. PMC 8828740. PMID 35140252.
- ↑ Cvejic, Erin; Birch, Rachael C.; Vollmer-Conna, Uté (May 2016). "Cognitive Dysfunction in Chronic Fatigue Syndrome: a Review of Recent Evidence". Current Rheumatology Reports. 18 (5): 24. doi:10.1007/s11926-016-0577-9. ISSN 1523-3774.
- ↑ Capuron, Lucile; Welberg, Leonie; Heim, Christine; Wagner, Dieter; Solomon, Laura; Papanicolaou, Dimitris A; Craddock, R Cameron; Miller, Andrew H; Reeves, William C (2006). "Cognitive Dysfunction Relates to Subjective Report of Mental Fatigue in Patients with Chronic Fatigue Syndrome". Neuropsychopharmacology. 31: 1777–1784. doi:10.1038/sj.npp.1301005.
- ↑ Michiels, V.; Cluydts, R. (2001). "Neuropsychological functioning in chronic fatigue syndrome: a review". Acta Psychiatrica Scandinavica. 103 (2): 84–93. ISSN 0001-690X. PMID 11167310.
- ↑ Tillman, Adriane (June 4, 2018). "Victory for ME Disability Claim - U.S. Court Upholds Plaintiff's Lawsuit After Being Denied Disability". #MEAction. Retrieved February 2, 2019.

